Syllabus

MA489 Options

MA325/326 Mathematical and Logical Aspects of Computing

• An appreciation of some of the mathematical and logical ideas and techniques which are useful in computer science.
• Boolean Logic, Path searching logic trees.
• Simple machines; Finite State Machines; Turing Machines.

MA401 Combinatorial Mathematics

• Permutations, combimations, compositions, partitions, generating functions for enumerations
• Polya's Enumeration Theorem, patterns, Polya's theory of counting
• Graph theory, network flows
• Block designs
• Applications to information theory, crystallography

References

• N.L.Biggs, "Discrete Mathematics" (Oxford)
• B. Bollobas, "Graph Theory" (Springer)
• D.I.A. Cohen, "Basic Techniques of Combinatorial Theory" (Addison Wesley)
• S. Lipschutz, "Discrete Mathematics" (Schaum Outline)
• H.J. Ryser, "Combinatorial Mathematics" (MAA)
• A. Tucker, "Applied Combinatorics" (Wiley)

MA402 Number Theory

• Divisibility, primes, congruences, residues
• Number theoretical functions
• Diophantine equations
• Continued fractions
• The distribution of primes
• Algebraic numbers

References

• A. Baker, "Introduction to the Theory of Numbers" (Cambridge)
• H. Davenport, "The Higher Arithmetic" (Hutchinson)
• G.H. Hardy & E.M. Wright, "An Introduction to the Theory of Numbers" (Oxford)
• T. Nagell, "Introduction to Number Theory" (Chelsea)

MA403 Category Theory

• Categories
• Functors, covariant and contravariant; natural transformations, adjoint functors
• Abelian categories, categories of modules

MA404 Algebraic Topology

• Homotopic mappings, fundamental groups, covering spaces
• Simplicial complexes, simplicial homology theory
• Mayer-Vietoris sequences, some applications of homology

References

• J.G. Hocking & G.S. Young, "Topology" (Addison Wesley)
• E.H. Spanier, "Algebraic Topology" (McGraw Hill)
• A.H. Wallace, "Algebraic Topology" (Benjamin)

MA405 Algebraic Geometry

• Noetherian rings
• Dedekind domains
• Valuation theory
• Local rings, polynomial and power series rings

MA406 Differential Geometry

• Differential manifolds, vector fields, differential forms, maps
• Frame bundles, parallelism, geodesics
• Curvature, torsion, structure equations, Riemann connections, sectional curvature

References

• S. Helgason, "Differential Geometry and Symmetric Spaces" (Academic Press)
• I.M. Singer & J.A. Thorpe, "Lectures on Elementary Topology and Geometry" (Springer)
• M. Spivak, "Differential Geometry" (Publish or Perish)

MA407 Differential Equations

• Linear systems
• Vector and matrix norms
• The exponential of a linear operator
• Canonical forms, and computation of exponentials
• Linear flows
• Sinks and sources
• Periodic and hyperbolic flows
• Existence and uniqueness of solutions of non-linear systems
• Dependence on initial conditions
• Global solutions
• The flow of a differential equation
• Non-linear sinks
• Stability
• Lyaponov functions
• Qualitative analysis of the differential equations for a predator-prey ecology, and an ecology of competing species

References

• M. Hirsch & S. Smale, "Differential Equations, Dynamical Systems and Linear Algebra" (Academic Press)

MA408 Lie Groups

• Complete fields
• Analytic manifolds
• Analytic groups
• Filtrations on standard groups
• Associated Lie algebra
• Representation theory

MA409 Computer Science

• Concepts in data processing
• Assembly language
• Concepts in systems analysis
• System programming

MA410 Artificial Intelligence

• Review of logic
• Propositional calculus, truth tables, conjunctive and disjunctive normal forms, arguments
• Predicate calculus, Skolemisation, clause form, resolution
• Searching: Breadth first, depth first and best first search in a state space
• Two-person games, the minimax procedure, alpha beta pruning
• Introduction to PROLOG
• Facts, rules, queries, back-tracking, lists
• Searching, production systems

References

• I. Bratko, "PROLOG programming for artificial intelligence" (Addison Wesley)
• G.F. Luger and W.A. Stubblefield, "Artificial intelligence and the design of expert systems" (Benjamin Cummings)

MA426 Fourier Analysis

• Fourier series. The Riemann-Lebesgue Theorem. The Dirichlet condition for convergence. The Gibbs Phenomenon. Fejer kernels and Cesaro summation of Fourier series.
• Fourier transforms on R. L₁ and L₂ functions. The Plancherel Theorem. Band-limited functions and the Shannon Sampling Theorem. convolution and filtering.
• Discrete Fourier transforms. The Fast Fourier transform and its applications. Digital filtering.

MA413 Applied Statistics (Prerequisite:MA387)

• Use of computer-based packages, including MINITAB and BMDP.
• Descriptive statistics. Exploratory data analysis. Graphical methods in statistics. Transformations of data.
• Standard statistical inference, applied to real data. Linear models, including ANOVA and regression.
• Multivariate methods, including discriminant analysis, principal component analysis and cluster analysis.

MA417 Automated Reasoning

• Propositional calulus: truth functions and propositional connectives, logical validity, an axiomatization and completeness meta-theorem
• First order theories: axioms, theorems, interpretations, logical validity
• Rules of inference: binary resolution, hyper-resolution, demodulation, subsumption, proof by contradiction
• The Set of Support Strategy (and weighting)
• Introduction to UNIX on Dangan workstations
• Using the OTTER computer package: puzzles, logic circuit design/validation, theorem proving
• A first order theory for Peano arithmetic
• Gödel's Incompleteness Theorem: statement, indication of proof (Gödel numbers, recursive functions, representable functions), relevance to automated theorem proving.

References

• E. Mendelson, "Introduction to Mathematical Logic" (Wadsworth and Brooks / Cole)
• L. Wos, R. Overbeek, E. Lusk and J. Boyle, "Automated Reasoning (McGraw Hill)

CS401 Fractal Geometry

• Iterated function systems; applications to image compression
• Self-similarity; graph self-similarity; random self-similarity; similarity dimension
• Topological and Hausdorff dimension; other empirical dimensions
• Chaotic dynamical systems
• Julia and Mandelbrot sets
• Lindenmayer systems; models of plant growth

References

• M. Barnsley, "Fractals Everywhere", (Academic Press)
• G.A. Edgar, "Measure, Topology, and Fractal Geometry", (Springer)

CS402 Cryptography

• Number theory: time estimates, finite fields and quadratic residues
• Cryptography: public key cryptography, RSA cryptosystems, the Diffie-Hellman (discrete log) key exchange system, knapsack method
• Primality and factoring: the Rho method, factor bases, the continued fraction method
• Elliptic curves: elliptic curve cryptosystems, elliptic curve factorisation

Texts

• N.Koblitz, "A Course in Number Theory and Cryptography" (Springer)

CS407 Computer Algebra

• The course provides an introduction to computational aspects of abstract algebra.
• Examples are given for how problems in algebra can be modelled on a computer, and how computer programs can be used to treat algebraic questions algorithmically or by experiment.
• An introduction to the GAP system and its programming language is given.
• Examples of topics include:
• Long Integer Arithmetic (representing arbitrarily large numbers on a computer, classical algorithms for addition, subtraction, multiplication, division and their implementation, complexity of the algorithms)
• Prime Numbers (primality test methods, trial division, Sieve of Eratosthenes, Pollard 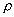 and Pollard p-1 method, Fermat's theorem and pseudo-primes.)
• Computational Group Theorey (examples of groups, group presentations, group actions and permutation groups, the Todd-Coxeter procedure, orbits and stabilizers, the size of a permutation group.)
• Practical exercises and homework form an essential part of the course.