Syllabus

MA250 Engineering

MA237/238 Statistics

• Descriptive statistics: collection and tabulation of statistical data, sources of statistical information.
• Frequency distributions and histograms, measures of location and dispersion

Probability:
• Definition of probability, the laws of probability, probability distributions, random variables, the binomial, normal and Poisson distributions, random sampling..
• Statistical estimation: unbiased estimators.
• Estimation of the mean and variance of a normal population, estimation of proportions,.confidence intervals for estimates.
• Statistical hypothesis testing: the principles of statistical tests, the 2 types of error, the OC curve, tests concerning means and variances, the 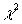 Test, goodness of fit, contingency tables. Correlation and regression.

T. Sincich. Business Statistics by Example. Dellen/Macmillan.

J.E. Freund. Modern Elementary Statistics. Prentice Hall.

P.G. Hoel & R.J. Jesson. Basic Statistics for Business and Economics. Wiley.  

MA251/252 Calculus

• Functions of 2 and 3 variables; the definitions of limits and continuity, partial differentiation, total derivatives
• Scalar functions, vector functions, vector fields
• The Chain Rule, the Jacobian matrix
• Equations of tangent planes and normal lines, extrema of scalar functions, maxima and minima of constrained functions, Lagrange multipliers
• Arc lengths, line integrals, polar curves
• Multiple integration: areas and volumes, Jacobians, change of variables, the Theorems of Green, Gauss and Stokes
• Functions of a complex variable: the Cauchy-Riemann equations, Cauchy's Integral Theorem, the calculus of residues, contour integrals
• Sequences and series: series of positive terms, the Ratio and Comparison Tests for convergence, alternating series
• Power series: functions defined by power series, their integrals and derivatives, Abel's Theorem

Texts

• G.B. Thomas & R.I. Finney, "Calculus and Analytic Geometry" (Addsison Wesley)

References

• S.L. Salas, E. Hille & J.T. Anderson, "Calculus, One and Several Variables" (Wiley)
• A.J.M. Spencer et al, "Engineering Mathematics" (van Nostrand Reinhold)

MA253/254 Algebra

• Rⁿ as a vector space: subspaces, linear independence, bases, dimension
• Linear transformations, the natural matrix and the matrix with respect to a given basis
• Eigenvectors, eigenvalues and diagonalisation
• Rⁿ as a Euclidean space, the Gram-Schmidt process
• Orthogonal reduction of a symmetric matrix
• Applications to recurrence relations, differential equations, Markov chains etc
• Introduction to matrix games

Texts

• J.B. Fraleigh & R.A. Beauregard, "Linear Algebra" (Addison Wesley)

References

• F. Ayres, "Matrices" (Schaum Outline)

MA255/256 Numerical Analysis

• Ordinary differential equations: Euler's method, the modified Euler method, extrapolation, predictor-corrector methods, Runge-Kutta methods, Taylor series methods
• Gaussian elimination: partial pivoting, round-off errors
• Eigenvalues and eigenvectors: location of eigenvalues, the power method, the inverse power method

Texts

• L.V. Atkinson, P.J. Harley & J.D. Hudson, "Numerical Methods with FORTRAN 77" (Addison Wesley)

References

• C. Dixon, "Numerical Analysis" (Blackie)
• C.F. Gerald & P.O. Wheatley, "Applied Numerical Analysis" (Addison Wesley)
• I. Jacques & C. Judd, "Numerical Analysis" (Chapman & Hall)
• R.E. Scraton, "Basic Numerical Methods" (Arnold)