Syllabus

AS200 Applied Mathematical Science

MA211 Calculus (part one)

• Methods of integration: substitution, integration by parts, partial fractions, reduction formulae
• Inverse functions
• Improper integrals (as limits of finite integrals)
• Differential equations: linear equations with constant coefficients, first order homogeneous equations.

MA212 Calculus (part two)

• Series: convergence, divergence, absolute convergence
• The Comparison, Integral and Ratio Tests
• Alternating series
• Power series, the Radius of convergence
• Functions of several variables, and vector-valued functions (in R^2 and R^3): vectors, scalar product, cross product in R^3, equations of lines and planes in parametric form
• Partial derivatives: gradients, tangent planes, maxima and minima of functions of 2 variables, Lagrange multipliers
• The Chain Rule

Texts

• G.B. Thomas & R.I. Finney, "Calculus and Analytic Geometry" (Addsison Wesley)
• S.L. Salas, E. Hille & J.T. Anderson, "Calculus, One and Several Variables" (Wiley)

MA203 Linear Algebra

• Systems of linear equations, the Gaussian (row reduction) technique
• Matrices, determinants, adjoints, inverses
• Row operations, inverse of a matrix by row reduction
• Eigenvalues and eigenvectors, diagonalisation of a matrix with distinct eigenvalues; application to Markov processes, transition matrices
• Orthogonal matrices, orthogonal reduction of 2 by 2 and 3 by 3 matrices; applications to quadratic forms

Texts

• J.B. Fraleigh & R.A. Beauregard, "Linear Algebra" (Addison Wesley)

References

• F. Ayres, "Matrices" (Schaum Outline)

MA204 Discrete Maths

• Enumeration: the Rules of Sum and Product, tree diagrams, inclusion and exclusion, combinations and permutations, distributions and selections
• Graphs: Euler trails and Hamiltonian cycles, properties of trees (including spanning trees, ordered rooted trees, and tree traversals), planar graphs, colouring problems, various algorithms, applications

Texts

• S. Lipschutz, "Discrete Mathematics" (Schaum Outline)

MA221/223 History

• The history of number theory
• The history of Pi
• Greek geometry
• The history of geometry
• The history of differential geometry
• The history of calculus
• The history of knot theory
• Sir William Rowan Hamilton
• Fermat's Last Theorem

References

• J. Fauvel & J. Gray (eds), "The History of Mathematics: A Reader" (Macmillan)
• D.J. Struik, "A Concise History of Mathematics" (Dover)

MP201 / MP202

MP255/MA256 Numerical Analysis

• Ordinary differential equations: Euler's method, the modified Euler method, extrapolation, predictor-corrector methods, Runge-Kutta methods, Taylor series methods
• Gaussian elimination: partial pivoting, round-off errors
• Eigenvalues and eigenvectors: location of eigenvalues, the power method, the inverse power method

Texts

• L.V. Atkinson, P.J. Harley & J.D. Hudson, "Numerical Methods with FORTRAN 77" (Addison Wesley)

References

• C. Dixon, "Numerical Analysis" (Blackie)
• C.F. Gerald & P.O. Wheatley, "Applied Numerical Analysis" (Addison Wesley)
• I. Jacques & C. Judd, "Numerical Analysis" (Chapman & Hall)
• R.E. Scraton, "Basic Numerical Methods" (Arnold)

MA237/238 Statistics

Descriptive statistics: collection and tabulation of statistical data, sources of statistical information.

Frequency distributions and histograms, measures of location and dispersion

Probability:

Definition of probability, the laws of probability, probability distributions, random variables, the binomial, normal and Poisson distributions, random sampling..

Statistical estimation: unbiased estimators.

Estimation of the mean and variance of a normal population, estimation of proportions,.confidence intervals for estimates.

Statistical hypothesis testing: the principles of statistical tests, the 2 types of error, the OC curve, tests concerning means and variances, the 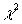 Test, goodness of fit, contingency tables. Correlation and regression.

T. Sincich. Business Statistics by Example. Dellen/Macmillan.

J.E. Freund. Modern Elementary Statistics. Prentice Hall.

P.G. Hoel & R.J. Jesson. Basic Statistics for Business and Economics. Wiley.